Recently my mother asked me, “What is calculus?”
After recovering from shock, my response to her was, “Asking that question was a big mistake!”
She laughed.
Mothers of the world, do not fear! I am here for you. You deserve to have your heavy burdens lightened. For the great cause of uplifting motherhood, I have prepared the following explanation.
What is calculus?
Most people know that three times four equals twelve. The equation can be illustrated graphically here:
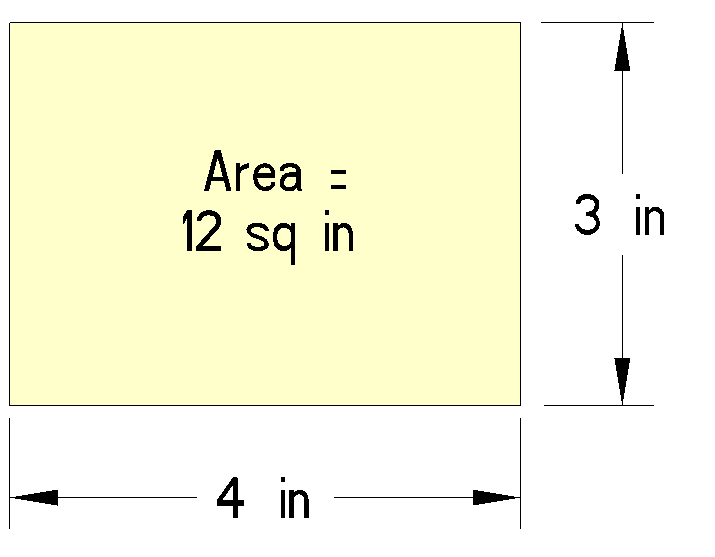
The rectangle’s area is calculated using the following equation:
3 inches x 4 inches = 12 square inches
If all relationships in the universe between distance, time, mass, and energy could be represented by rectangles, there would be no need for calculus. Unfortunately, such is rarely the case. Tree trunks and limbs have curved shapes. Mountain ranges and rivers meander in great, swirling arcs.
A practical example
A young woman walks four hours from her home to her babysitting appointment. She is a very dedicated babysitter (and future mother)! Fearing she may arrive late for her appointment, she walks faster the closer she gets to her young clients.
At the start of her walk, her pace is 1 mile-per-hour. By the time four hours has passed, she has increased her speed to 3 miles-per-hour.
The question is, how far did the babysitter walk from her home to her appointment?
How far something has traveled over a period of time is calculated by multiplying how fast it traveled by how much time it traveled:
Speed x Time Traveled = Distance Traveled
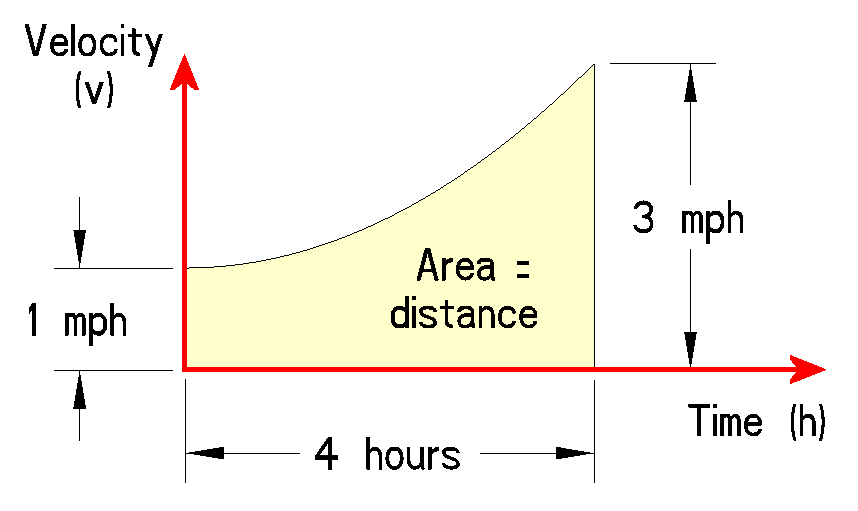
But in this example, the girl’s walking speed changes over the four hours. WHICH velocity do we use as the "Speed"? 1 mph, 3 mph, or or something in between?
1 mph x 4 hours = 4 miles walked
2 mph x 4 hours = 8 miles walked
3 mph x 4 hours = 12 miles walked
Which of the three is the correct length of her walk? Or are any correct?
The area of the yellow oblong shape shown above is equal to her distance walked. What is that area of that shape?
This is where calculus comes in.
To accurately calculate her distance walked, we must complete two steps:
Precisely describe the curve at the top of the rectangle.
Apply calculus.
STEP 1:
Unfortunately, the equation that describes her walking velocity (v) over time (hours = h) is complex. The upward-swooping curve is described by the following equation that describes her pace at every step within her 4-hour walk.
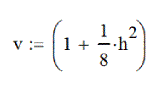
For this discussion, you don’t need to understand the above equation. But you must believe that SOME equation is required to describe that curve.
STEP 2:
Calculus allows the equation to be placed into an integral, as depicted below:
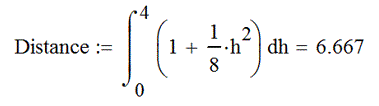
Again, my intent is not to explain HOW to use calculus, but rather to explain WHAT calculus does.
People practiced in calculus can solve the above equation on paper without a computer or calculator.
The answer to the question, “How far did the young woman walk?” is 6.667 miles.
A true story
I hated math when I was in high school. I took only the minimum mathematics courses required to graduate from high school. Not a single extra addition problem for me!
However, by the time I entered college I had decided to become an engineer. Needless to say, I had some catching up to do. But the day came when I stepped into my first calculus class. That was when I realized all math points to calculus.
Calculus connects lifeless numbers and symbols to our living world. Calculus is the breath of life of mathematics.
"I never use this math"
While we're on the topic of hating math, what is the best response to young people who say,
"Why do I have to take this math class? I'll never use it."
Recommended response:
"You don't know if you'll need this math or not
because you don't know what career you'll have."
That is the honest truth! Even after being admitted into colleges or universities, students often change majors until finally settling on one. Students in 7th through 12th grades have very little insight into what their profession will be. Therefore, it is unwise for them to assume the math they're learning won't be used later in life.
Calculus,
Describes the path of a thrown baseball
Explains why trees are shaped the way they are
Predicts how fast air leaks out of a girl’s bicycle tire
Creates equations used in financing, medicine, and business
Predicts the strengths of structures such as buildings and bridges
Predicts the distribution of the circulatory systems within our bodies
When astronauts reach the center of the galaxy, they will find it filled with calculus equations.
Calculus is as close is as we get to magic in real-life. All mothers could use more magic.
Comments